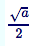
| 右を見てください。同じ数式(a の平方根を2で割った分数)が2つ並んで見えていますか? そうでない場合にはあなたが今使っているブラウザは数式表示のための規格 MathML に対応していません。 現時点で対応しているのは, Firefox, Google Chrome, Safari, Opera ですので,どれかをインストールして使ってください。 | $ \frac{\sqrt{a}}{2} $ |
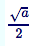
|
状態の変化や物体の運動のような「変化」は,一般に微分方程式を用いて 記述され,それを解くことで将来の予測が可能になります. 次はよくある微分方程式の形です.
| (1) 微分方程式: | \[ \frac{d x}{d t} = f(x,t) \] |
|---|
この式の意味は,対象としている量 $ x $ の値の 変化が, 現在の時刻とその量の現在の値とで決まる関数の値によって決まるということです. ちょっと分りにくい表現ですが,実例が後で出てきますので,とりあえずさらっと読んでください.
このような 微分方程式が, 解析的に,つまり式の変形などの数式の操作によって解くことができるならば ,数学的に完全な答を導くことが出来るのですが,通常そうはいきません. せっかく微分方程式を立ててみても,解けないというケースが 非常に多いのです.
そこで,本来なら無限に短い瞬間($d t$)ごとの変化($dx$) で記述される微分を短い有限の時間のきざみ($\delta t$)ごとの変化($\delta x$)に置き換えてしまい,これを コンピュータを用いて繰り返し計算で計算することで, 実用上差し支えない精度の結果を得ようというやり方がとられています. このように有限の時間の刻みを用いるやり方は,微分に対して差分と呼ばれます.
| (2) 差分方程式: | \[ \frac{\delta x}{\delta t} = f(x,t) \] |
|---|
| \[\delta x = f(x,t)\times \delta t \] |
|---|
ところで,自然界でおきる現象の中には,世代ごとに形質が少しずつ変化していく 生物の進化のように,段階的な変化が積み重なっていくようなケースも あります.進化生態学では,生物個体の数が対象になるので, その意味でも不連続な取り扱いが適切だという側面もあります. したがって, この場合は本質的に差分が使えるという考え方もできます.
しかし,世代ごとの形質の変化は微小であり, 一方で生物個体の数が多いためにその変化が連続である とみなせることから,この種の問題も基本的には微分の問題として 取り扱われています.シミュレーションではそれをまた差分化して解くわけです. 回りくどいやり方ですが,このようなやり方で問題を抽象化,一般化 できるわけです(最近では個々の生物個体をじかに仮想的な個体として コンピュータの上に再現して,それらに自立的な行動をさせる, マルチエージェント手法も盛んになっていますが,これはいわば原点に 戻った考え方です.ある意味分かりやすいのですが,解明に抽象性が欠けてしまいがちで,本質を とらえにくい欠点も持っています).
ある生物種の個体数を $x$ としましょう. 時間経過を$t$とし, 単位時間ごとに$x$のうち $k$ の割合は減少してしまうものとします. これは時間刻みを世代としたときに, 人口が一定の割合で減少することを意味しています. このとき人口の変化のようすは 次の微分方程式で表されることになります.
| (3) | \[ \frac{d x}{d t} = -kx \] |
|---|
この微分方程式は解析的にも簡単に解けて,次のような解を持ちます.
| (4) | \[ x = x_0 e^{-kt} \] |
|---|
ここで $t_0$ は時刻 $t=0$ の時の $x$ の値です.
式(3)を数値的に解くことを考えましょう. 微分は変化率を無限に短い時間の極限値で考えるのですが,コンピュータは 有限の時間しか扱えないので,「十分に短い」時間の刻みを考え, それ を$\delta t$とします. その間の $x$ の増加量を $\delta x$ と置くと, 式(3)は次のように近似できます.
| (5) | \[ \frac{\delta x}{\delta t} = -kx \] |
|---|
この左辺はもはや単なる分数ですから,次のように変形しても構いません.
| (5) | \[ \delta x = -kx \delta t \] |
|---|
式(5)は,有限の短い時間 $\delta t$ の間の $x$ の変化量 $\delta x$ を 掛け算の形で 求める式になっています.したがって 具体的に必要な値を定めてやればその間の変化を算出できます. その計算を何回も繰り返してやれば,長時間にわたる変化を計算することが できるわけです.
それでは実際に計算を行う手順を考えます.
あっけないほど簡単ですね.このようなやり方を Euler 法といいます.ちなみに Leonhard Euler(オイラー,1703-1783)は歴史上最大の数学者の一人で,数え切れないほどの定理や式を世に出したので, Euler の式とか Euler の定理というのも山のようにあります.彼の著作集は現在でも 出版事業が進められており,現在までに74巻が完結し,14巻が出版途中,それでも まだ残されているものの出版を準備中だそうです.すごいですねえ.→出版計画
上の例をプログラムで記述してみましょう.Ruby で書いたソースは次のようになります.なお,このプログラムには小さな問題点があり,その解説を下に書いてあります。
#!/usr/local/bin/ruby
# euler1.rb : 人口が減少する変化を追う
x_start = 10000.0 # 最初の人口
t_start = 0.0 # 最初の時刻
t_end = 100.0 # 最後の時刻
dt = 0.1 # 時間の刻み(分)
k = 0.05 # 減衰の速さを決める定数
t = t_start
x = x_start
nstep = ((t_end - t_start)/dt).to_i
for i in 0 .. nstep
printf("%8.6f %8.6f\n",t,x)
t += dt
x += -k * x * dt
end
さて,これを走らせて得られた結果を図示すると次のようになります.
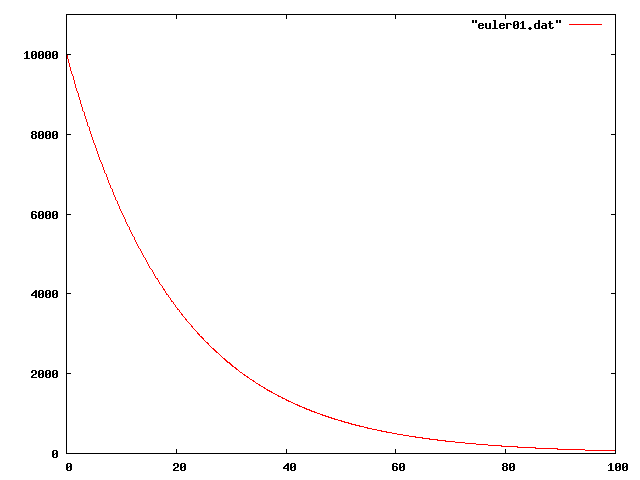
ここで扱っている微分方程式
\[ \frac{d x}{d t} = k (x - x_e) \]は解析的に解くことが出来て,その解は次のようになります.
\[ x = (x_0 - x_e) e^{-k t} + x_e\]この解が妥当なものであることは, $t = 0$ と置いたときと $t \rightarrow \infty $ としたときの$x$の値から納得できますから,自分で 考えてください.
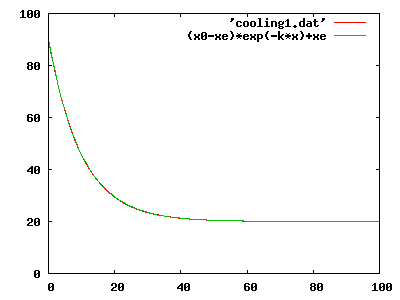
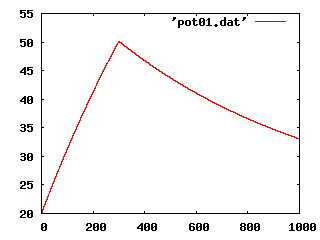
さて,この解析的な解も上の数値解と一緒にグラフにプ
ロットしてみたのが下の図です.2つのグラフがよく重なっていることから,Euler 法がかなり満足すべき解を
与えていることが分ります.
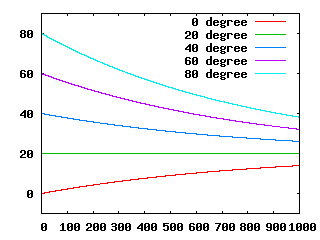
お湯の量: 1000.0 g, $C $ : 5.0 J/(℃$\cdot$s),室温 20 ℃, 追跡する時間: 1000 秒この場合について,上と同じように冷却問題を解きなさい。 ただし,今度は初期温度を 0.0℃,20℃,40℃,60℃,80℃として,それぞれの 初期温度についての解を求めてグラフに表示しなさい。
注: 1 J の熱を与えられると, 1 g の水の温度は 0.239℃ だけ上昇する。
| t の正確な計算法は? |
|---|
上のプログラムでは,時間 t を計算するのに,
ループが回るたびにdt を加算していくというやり方(t += dt) をとりました。
しかしこのやり方には問題があります。なぜなら,数を非常に
多数回加算することは,誤差の蓄積につながるからです。x の
値については,アルゴリズムの性質上,加算で求めるしかないのですが。
t については,むしろ
次のようにして求めるのが,
高い精度の計算のために適切なのです。
t = t_start + i * dtこのことを確かめるには,次のテストプログラムを走らせてみると よいでしょう。
dt = 0.01
t = 0.0
nstep = 1000000
for i in 0 .. nstep
t += dt
end
printf("%20.18f %20.18f\n",t,dt*nstep)
|
プログラムの書き方は各人各様で,正しいプログラムというのは何通りも あります.以下のプログラムはそのひとつの例として 提示したものです.ただし,合理的な書き方はこうあるべきであるという 指針にもなっているはずですので,参考にしてください.
なお,グラフについては,正しいプログラムであればほぼ同一の値が 出るはずです.もしグラフにちがいがあったら間違いと思ってよいでしょう( たまには模範解答の方がちがっていたりしますが).
小波秀雄, 2005/10/19