Euler 法を改良する — Leap-Flog 法

ここではまず Euler 法の問題点を調べて，それを改善するための より高い近似法である Leap-Frog 法を使ってみます． その後，物体の落下の問題を取り扱います． これらは力学的なシミュレーションの基礎となるものです．

Euler 法の問題点

Euler 法の区間の刻みを粗くしてみる

上の図を見てください．赤はある微分方程式を解析的に正確に解いて 得られた曲線です．その下側にある折れ線は，非常に大きな間隔を 使って Euler 法で同じ微分方程式の解を求めたものです．正しい 曲線に比べて，Euler 法では解が小さな値をとってしまっていることが 分ります．その原因はどこにあるのでしょうか．

グラフの左下は，計算の出発点です．本来の解と，Euler 法による解とは， 出発点での向きは一致しています．Euler 法による解は，そのまま直線で 延びているのに，正しい解の法は，そこから上向きにカーブしています．この 違いが問題だということは，見ればわかります． つまり，Euler 法は，

• 傾きを使って次の点を予測する
• カーブによるずれは計算に入れられない

Euler 法の詳しい検討

下の図を使って，そのことを詳しく説明してみましょう． 解かれるべき微分方程式は

$\frac{dx}{dt} = f(x,t) $

$x = F(t)$

このグラフを見るとき，横軸は $ t $，縦軸は$ x $ になっているこ とに注意してください(グラフはいつでも 横軸が $ x $，縦軸が $ y $ だと思わないように！)． $ t $ は時刻， $ x $ は位置ということにして説明します．

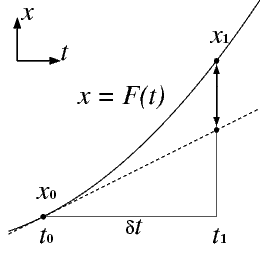
いま，時刻$ t_0 $ で 位置が $ x_0 $ にあったとしましょう． この点でのグラフの傾きは，定義によって $ f(x_0,t_0) $ で す．図の点線の傾きがちょうどそれになっていることは 見ればわかるでしょう． この時点から ある短い時間 $ \delta t $ が過ぎた時刻 $ t_1 $ での 位置を予測したいのです． その計算方法は簡単で，

上昇の幅＝傾き×水平のずれ

$f(x_0,t_0) \delta t $

$ x_1 = x_0 + f(x_0,t_0) \delta t $

ところが，こんなふうにして得られた点は，本当の解の曲線上には乗ることが できず，ずれが生じてしまいます．図の矢印は真の解における 位置 $ x_1 = F(t_1) $ と，上の計算で得られた 答とのずれを示しています． このように，Euler 法は解となる曲線が曲がっていることを 考慮しない計算法なので，そのことによるずれは避けられません．

もっともこれでも 間隔を十分に細かく取って計算してやれば，正確な解にいくらでも 近い結果を得ることが，原理的にはできるはずです．なぜなら， 自然は瞬間瞬間の傾きから，その次の無限に近い点を決めて動いている といってもよいのですから．

ところが，このような差分法を非常に細かい区切りで実行することには， 次のように2つの問題点があります．

• 回数が莫大になってしまって，計算時間が非常に長くなる．
• 膨大な数を足しあわせていくことになり，誤差の蓄積によって計算精度が落ちてしまう．

Leap-Frog 法

Euler 法の原理を微分形で表す

時間 $ t$ とともに変化する量 $ x $ が次の微分方程式に従うものとします．

$ \frac{dx}{dt} = f(x,t) $

まず$ t$の 関数$F(t) $ の微分の定義というのは， 通常次のように表されます．

$ \frac{d F(t)}{dt} = \lim_{h \rightarrow 0} \frac{F(t+h)-F(t)}{h} $

$\frac{F(t+\delta t)-F(t)}{\delta t} = f(x) $

Leap-Frog 法の原理

さて，ここで微分の定義を次のようにひとひねりして書いてみます．

$ \frac{d F(t)}{dt} = \lim_{h \rightarrow 0} \frac{F(t+h)-F(t-h)}{2h} $

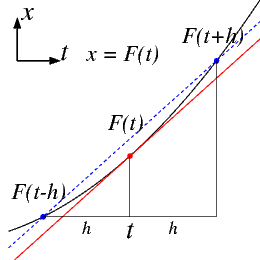
Leap-Frog 法は上記のような微分形を差分化したものと 考えることができます． $ h $を有限な刻み $ \delta t $ に置き換え，さらに $ t-h \rightarrow t_0 $, $ t \rightarrow t_1 $, $ t+h \rightarrow t_2 $， $ F(t-h) \rightarrow x_0 $, $ F(t) \rightarrow x_1 $, $ F(t+h) \rightarrow x_2 $ という置き 換えを行ったのが下の図です．

これを使った差分方程式の形は次のようになります．

$\frac{x_2-x_0}{2 \delta t} = f(t_1) $

$x_2 = x_0 + 2 f(x_1,t_1)\delta t $

$ t = t_1 $ における接線の傾きは $ f(t_1)$ です．この接線を上にずらしてやって， ちょうど $ x_0$の点を通るようにしてやります．その点から $ 2 \delta t $ だけ進んだところでの 上昇分 $ 2 f(t_1) \delta t $ を $ x_0$ に加えると，$ x_2 $ の値に近い値が得られるはずです．

このやり方では，$t = t_0 $ からの増加分を求めるのに， その時点での微分係数 $ f(t_0)$ を用いずに， 目的とする点までのちょうど半分のところでの 微分係数を使っています．ですから，曲線の曲がりの効果も 計算に含まれることになり，計算の精度は改善されることになります． Leap-Frog 法の精度についての説明は下に示してありますから，参考にしてくだ さい．

Leap-Frog 法は初期値のとり方に工夫がいる

実際に Leap-Frog 法をプログラムに組み込もうとすると， Euler 法にはなかった問題点にぶつかります．それは， 初期値が1つではすまないということです． つまり，Euler 法では最初の時刻 $t =t_0 $ での $ x = x_0 $ の値さえ分れば，それら を $ f(x,t)$ に代入して $ f(x_0,t_0)$ を得て，それから 傾きを計算することができました(お湯の冷却問題では， $f(x,t) $ は $t$ には依存しないので，単に $f(x) $の形になっています)．ところが Leap-Frog 法では，次の点の値を予測するために必要な 傾きは $ \delta t$ だけ進んだ時点 $ t = t_1 $ での傾きなのです． その瞬間の$x $ の値は $ x_1 = F(t_1) $ なので すから，そもそも $ F(t)$ を求めようというのに，先にその解を 知らないといけないという自己矛盾が発生してしまいます．

上記の難点を切り抜けるためには， とりあえず Euler 法のやり方で $ x_1 $ を求めてしまおうというやり方を 取ることにします．つまり，$ t = t_0$ の時の 傾き $ f(x_0,t_0) $ を使って，次のように $ x_1 $ を求 めるのです．

$ x_1 = x_0 + f(x_0,t_0) \delta t $

Leap-Frog 法を実装する

Leap-Frog 法を実装するために，その手続きを書き並べてみます．

• 最初に与えられているもの： 初期値 $ t_0, x_0$， 求めるべき関数 $F(t) $ の変化率を規定する関数 $ f(x,t)$
• 決めておくべき定数： 時間刻み $ \delta t$ と 計算すべき $t $ の範囲． ただし， 計算すべき範囲と，それをいくつに分割するかという，区間の数を決めておいてもよい． その場合，$ \delta t$ は割り算で決めることになる．
• $ x_1 = x_0 + f(x_0,t_0) \delta t $ を使って $ x_1 $ を求める．
• $ x_0, x_1 $ を $x_2 = x_0 + 2 f(x_1,t_1)\delta t $ に代入して， $ x_2$ を得る．
• $ x_1, x_2 $ を $x_3 = x_1 + 2 f(x_2,t_2)\delta t $に代入して， $ x_3$ を得る．
• 以下必要な回数だけ繰り返す．

#!/usr/local/bin/ruby
def f(x)      # f(x,t)，ただし，この場合には f は t に依存しない． 
  return 0.1 * x
end
tstart = 0.0  # 始まりの時刻
tend = 10.0   # 終了時刻
xinit = 1.0   # x の初期値
nstep = 10    # 分割区間の数
dt = (tend-tstart)/nstep
dth = dt/2    # dx の半分
t = tstart
x0 = xinit
x1 = xinit + dth * f(x0)   # 最初に x1 を求めておく．
for i in 1 .. nstep
  printf("%12.9f %12.9f\n",t,x0)
  printf("%12.9f %12.9f\n",t+dth,x1)
  x2 = x0 + dt * f(x1)
  x3 = x1 + dt * f(x2)
  t = tstart + i * dt
  x0 = x2
  x1 = x3
end

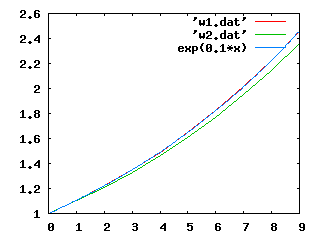
このソースを使って実際に計算した結果を下に示します． 赤が Leap-Frog 法による結果，青は解析的な厳密解，緑は Euler 法による結果です．Euler 法に比べて格段に精度が 向上していることが分ります．

元に戻る

小波秀雄, 2005/10/19