会社に出社して、今日の仕事のための資料を引き出しから出そうとしたら、ない!あちこちありそうなところを探すのだが出てこない。探しながら「ひょっとして誰かが勝手に持ちだしたんじゃ・・・」という疑念が湧いてきた。同僚たちはみないい人だとはわかっているけど、しかし、だんだん募る人間不信と、人を信じることができない自己嫌悪にさいなまれるメロスのような心境が、一箇所開けるごとに湧いてくる。できれば人を疑いたくない。それでも最後の探し場所にもなかったら、他人を疑うしかないだろう。
こういう状況は、程度の差やシチュエーションの違いこそあれ、だれしも経験があるのではないだろうか。私などは家の中で何かをなくしてさんざん探しまわりながら、だんだんに娘の顔が浮かんできて、「まったくもう、子どもの教育を誤ったよ」とつぶやきながらの捜索になるのだが、外出から戻ってきたかみさんは、私が探しものをしていることを一目で見抜いて、「それ、ここにあるよ」と指差すのがたいていの結末である。自分のダメさ加減を噛み締めながらも、娘に濡れ衣を着せなくて済んだと胸をなでおろすわけだ。「七たび探して人を疑え」ということわざを噛み締めながら。でもたまには、愛用の精密ドライバーセットを娘に持って行かれていたりすることもないではない。
こんなとき、どれくらいまでは人を信じていていいのだろうか?つまり、半分まで探しものの捜索を終えた時点で見つかっていなければ、他人のしわざである可能性が高いと思っていいのか、あるいはもっと少ない段階か、はたまたぎりぎりまで自分で見つけられるはずと楽観していいのか。その問題を考えてみよう。
話を簡単にするために、自分が探している物が入っている引き出しの数は 20 であるとする。引き出しでも棚でもキャビネットでもまとめて「引き出し」だ。もうひとつ、誰かがそれを持ち出している可能性を 0.01 としよう。100回に1回くらいは、魔が差した同僚がちょいと持って帰ってしまうこともあるだろうというわけだ。この条件で、\(x\)番目の引き出しまで開けて全部空だったときに、大事な資料が誰かに持ち去られた確率がどうなるを考えよう。
ちょっとややこしく聞こえるかも知れないがたとえばこんな感じで考えればよい。
自分はもう 10番目まで引き出しを開けてみたが、まだ見つからない。ひょっとして誰かが持ち帰ってしまったのだろうか?とすると、その確率はどうなんだろう。
つまり、どんどん開けていっても見つからない時に、いつ、どの程度疑心暗鬼になっていいのだろうか?ということを考えたいのだ。
前提として、次のように考えよう。
- 書類を誰かが持ち去っている可能性は100分の1としよう。悪い人はめったにいないという性善説だ。
- 探しものは20個の引き出しのどこかにランダムにあるとする。
計算の詳細は飛ばして、結果の式を示すと次のようになる。99とか20という数字がどこから来ているのかは、上の設定を見るとすぐにわかると思うので、興味のある人は数字を入れ替えてみて試してみてください。
$$ P(A|E) = \frac{1}{1+99(1-x/20)} $$
次のように事象が定義してある。
\(A\) : 探しものはここにはないという事象
\(E\) : \(x\)番目まで開いて見つからなかったという事象
つまり、\(P(A|E)\)は \(x\)番目まで開いて見つからなかった時に、実は探しものは誰かが持ち去っているという確率だ。 計算結果を示すと下のグラフのようになる。
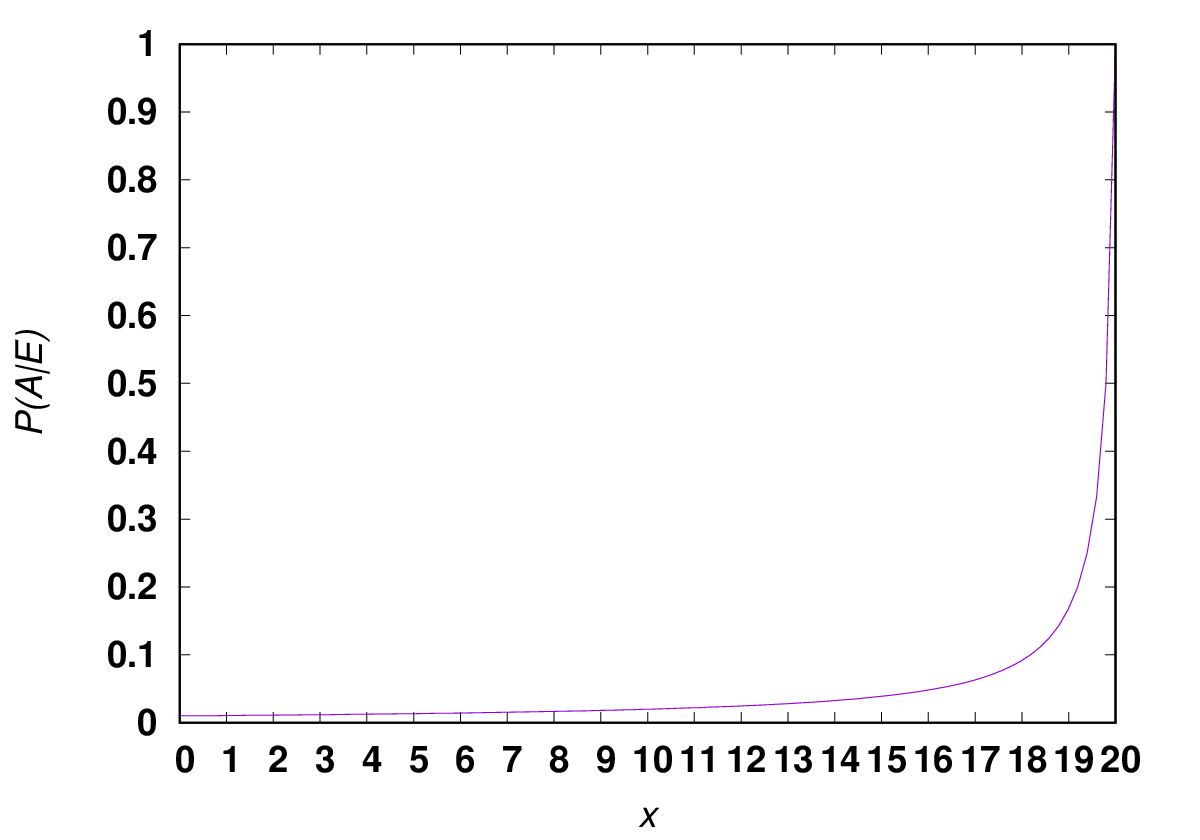
このグラフの意味を考えよう。\(x=0\) つまりまだ引き出しを開いていない時には、誰かが勝手に資料を持ち出している可能性は 0.01 しかない。当然だね。次に最初の引き出しを開いてそこになかったとしても、誰かが持って行っているという可能性は同じようにごく小さいと考えてよい。
さて、普通の忍耐力の人だったら、10番目位まで開けてみてやはり見つからないとなると、疑念が頭をかすめるのではないだろうか。しかし、グラフを見るとそれでも、人を疑わずに次の引き出しを探したほうがいいよ、君が悪さされている可能性は 0.03 ぐらいしかないよ、と、あくまで自分で探してみるようにというアドバイスが聞こえてきそうだ。
さてその先も開けていって、18番目まで開けたが、やっぱり出てこないというところで、ようやく1割ぐらいは人を疑ってもよさそうということになる。19番目でも出てこなかったら、急にそれが2割ぐらいにまで上がる。それにしてもなんという寛容な忍耐心を要求されることか!!
そして、20番目も空だったということになると、確率は1。当たり前だけど、まちがいなく誰かが持ち出していると判断することになる。
ということで、「七たび探して人を疑え」なのである。