高校の化学と生物では浸透圧について扱います。それどころか,中学理科の教科書にはないのにもかかわらず,中学入試でも浸透圧はたびたび登場するようです。現象としてどんなことが起きるのかという記述自体はべつだんむつかしいところもないので,リード文で解説を書いた上で出題できるわけですね。
「ナメクジに塩」とか「青菜に塩」といった,生活に密着した話題にもなるので,浸透圧ということば自体は,多くの人が知っているようです。まさに国民的理科用語です。
さて浸透圧については高校の化学と生物で学ぶことになっていて,大抵の教科書には次のような絵と文章で説明されています(絵は英文のWikipediaの絵を改変)。
真ん中を溶媒のみ通過させる半透膜で仕切ったU字管を用意し,その左右に水を入れると水平になったところでバランスする。その後一方にスクロース(ショ糖=砂糖の主成分)を入れて溶かすと,スクロース溶液のほうに水が移動する。これを浸透といい,しばらく放置すると高さの差が生じて止まる。このときの水圧の差を浸透圧という。

高校化学の教科書ではこのように現象が説明されて,そのあと簡単に理由が示されます。手元の教科書を見ると次のように「仕組み」が書かれています。
- これは,水分子だけが半透膜を通って水溶液側に拡散するために起こる(数研出版)
- 全体の濃度が均一になる方向に,溶媒が半透膜を通って濃度の低い方から高い方へ移動する(実教出版)
なお,生物の教科書(数研出版)には,上のような仕組みの説明はありません。
ファント・ホッフの式が登場
その後,化学の教科書では浸透圧に関する有名なファント・ホッフの式が紹介されます。
$$ \Pi V = n R T$$
ここで,\( \Pi\) が浸透圧で,\(V, n, R , T\)はそれぞれ 体積,物質量(昔の言い方ではモル数),気体定数,絶対温度を表します。この式は,一度でも化学を勉強したことのある人なら,理想気体の状態方程式とまったく同じであることに気づいているでしょう。
ところが,教科書には,ファント・ホッフの式が成立することの意味が,まったく書かれていません。またネット上の解説にも見当たりません。実は,浸透圧の式を物理の基本原理,この場合には熱力学から導き出すためにはかなり深く勉強しなくてはならないのです。例えば『熱力学 現代的な視点から』田崎晴明(培風館 2000)に詳しい導出がありますが,物理を専攻する学生でもかなり手ごわい。身近に観察できるし,生物とも関係が深い重要な現象であり,しかもファント・ホッフの法則が明快に見えて,初等的な化学や生物の教科書でも扱われているのですが,理論的にはいまひとつわからない印象を与えてしまっています。
平衡の概念を使って浸透圧を考える
おどしめいたことを書きましたが,浸透圧に理想気体の状態方程式と同じ形が現れることの定性的な説明は可能です。そのポイントは,浸透圧とは平衡状態において現れる圧力であるというところです。
次の図に浸透圧が働いているようすを示しました。青で表した水分子が左右にあり,左側には赤で示した溶質分子があります。溶質分子は中間の膜を通過できず,水分子は通り抜けることができます。左の液面には,大気圧以外に重りによる圧力がかかっていますが,もしもこの重りがないと,水分子は左側に移動して液面が上昇します。
重りがない場合に左の液面が持ち上がるのはなぜかは,下の結論を先取りして使う必要があります。重りがなくて膜に衝突する分子の圧力が等しいときには,膜の両側の分子の衝突による圧力は,右側では溶媒の水分子によるものであり,左側では水分子と溶質の両方の分子の衝突によるものです。それらが等しいのですから,水分子の衝突は右から左へ向かうほうが多い。都合,左への移動が優越することになります。浸透現象を,溶質が水分を引きずり込むからであると考える人は多いのですが,それは実はちがいます。
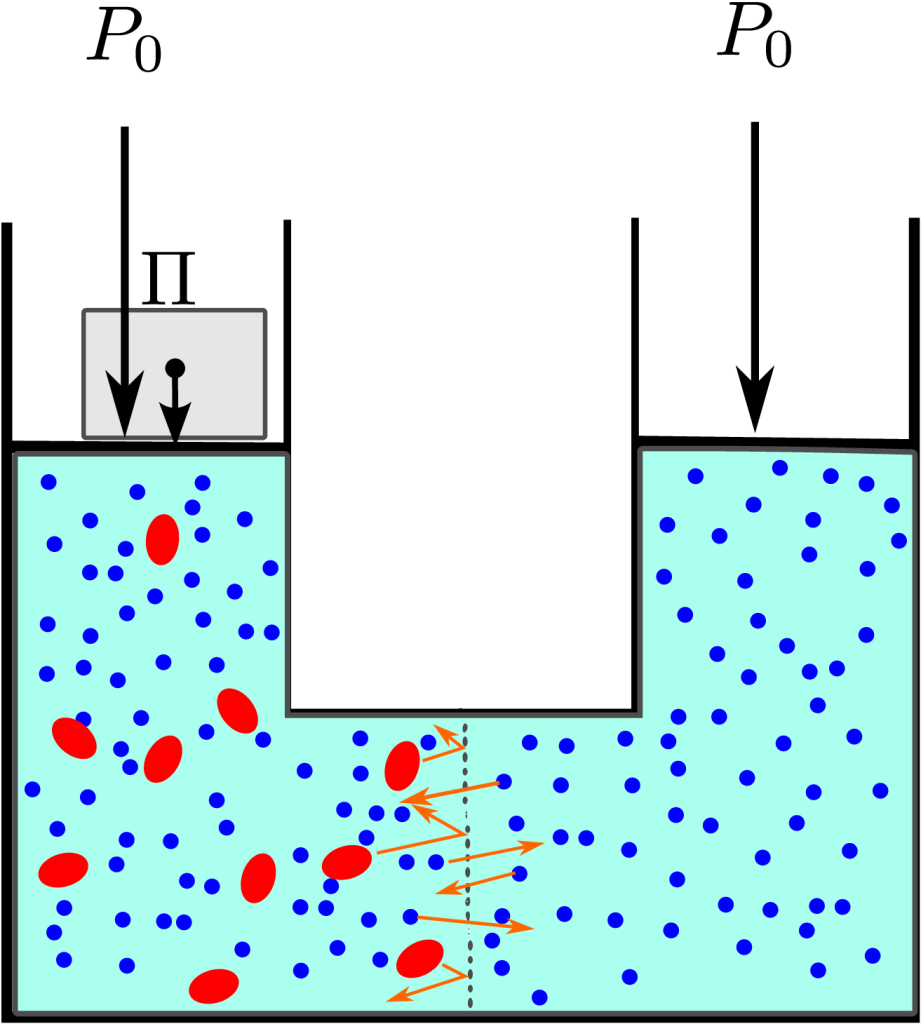
さて,上の図にあるように,圧力がつり合っているときの両側の圧力の関係は,左右の水面に同じ大気圧 \(P_0\)がかかっており,左側には水分子の移動を食い止めるための余分の圧力として浸透圧 \( \Pi\)が付け加えられています。
この状態が平衡状態であることに注意してください。平衡状態では膜を通した左右への分子の移動がつり合っています。膜に及ぼされる圧力は,左右からの分子の衝突によるものですから,平衡では水分子の衝突による圧力の分は等しく\(P_0\)になっているはずです。従って,浸透圧 \(\Pi\)は左からの溶質分子の衝突による圧力によって生じていると考えていいでしょう。
このことと,ファント・ホッフの式を考え合わせると,浸透圧は溶質分子が膜に衝突する時に生じる圧力であり,溶質分子が与える力は,理想気体の分子が壁に衝突する時に与える力と同じであろうということが推論できます。
溶液中の溶質の分子は,まわりの水分子と衝突して動き回っています。それが高分子などのコロイド粒子であればブラウン運動をしているようすを観察することもできます。それらが膜に衝突して及ぼす力と,自由な空間を飛び回っている気体分子が壁に当たって生じる力は,ファント・ホッフの式が成立することから考え合わせると同じであるというわけです。
物理学の法則は経験則である
以上の推論はファントホッフの式が成立することを物理の基礎理論から証明したものではありません。
一方,理想気体の状態方程式が成立することは,分子運動に関する力学的仮定から導き出すことができて,どうしてボイル・シャルルの法則が成立するかの説明を納得することができます。そのようなやり方で「どうして希薄溶液の浸透圧においては理想気体と同じ形のファントホッフの式が成立するのか?」という説明を与えることは,上の考察で得られるわけではないのです。
それでも,ファントホッフの式が成立するからには,「希薄溶液中の溶質分子は理想気体の分子と同様の運動エネルギーをもってランダムに動く粒子とみなしてよいだろう」ということを教えてくれるわけです。これはとても大きな内容をもっていて,このことを前提として,ブラウン運動をしている大きなコロイド粒子さえも,同様のエネルギー分配則にしたがうこと,そしてアインシュタインが示したように,ブラウン運動の測定データから普遍的な物理定数であるアボガドロ数を求めることさえできるのです。
もともとファントホッフの式が成立することは,実験と観察の結果であって,理論から導き出されたものではありません。しかし物理法則はすべて,経験的に得られたものであって,それらを定量的な法則の体系にまとめ上げたものが物理学です。その体系からまた演繹することで新たな法則が得られることもありますが,それは実験事実で検証されない限り「一人前の法則」とはみなされないでしょう。場合によっては基礎理論とデータが矛盾することさえありえて,そうなると物理の革命が起きて新しい物理学が誕生することさえあることは,量子力学の誕生についての科学史をかじった人なら知っています。
つまり,浸透圧におけるファントホッフの式を「理解」することは,それがなぜ成り立つのかを理解することとは若干ことなります。それは熱力学を基本から学ばないとむつかしい。しかし,上に述べたように,ファントホッフの式が経験的に成立することは,溶液中の分子の熱運動と理想気体の分子の熱運動に深い結びつきがあることを示しているのです。このことは,教師が教室で浸透圧を教えるときに熱を込めて伝えたいことだと思います。